class: center, middle, inverse, title-slide # Comparing numerical data ## Research methods ### Jüri Lillemets ### 2021-11-27 --- class: center middle clean # Are the numbers different enough? --- class: center middle inverse # The idea behind comparing numbers --- ## One sample T-test Assumptions: - normality - independence --- Let's use "Diameter, Height and Volume for Black Cherry Trees". The mean height of trees in our sample is 76. Is this different from some hypothetical population mean value? <!-- --> --- It would be reasonable to guess that mean tree height in population is be 75 ft. <!-- --> --- However, if we would be much more uncertain to estimate that the mean tree height in population is 74 ft. <!-- --> --- Another way to ask this: does the samples come from a population with a mean tree height of 74 ft? <!-- --> --- So our statistical hypothesis would be `\(H_0: \bar{x} = \mu\)` `\(H_1: \bar{x} \neq \mu\)` or `\(H_0: \mu = 74\)` `\(H_1: \mu \neq 74.\)` Let's set significance level `\(\alpha = 0.05\)`. --- We can see that there are several parameters that influence our guess: .pull-left[ - mean value of sample, `\(\overline{x}\)`; - our guess of sample mean, `\(\mu\)`; - standard deviation of the sample mean, `\(s\)`; - number of observations, `\(n\)`; ] .pull-right[ <!-- --> ] -- > How can we take all of these parameters into account? --- We combine these parameters into a test statistic! -- For this test the test statistic is called `\(t\)` and it's calculated as `$$t = \frac{\bar{x} - \mu}{s \div \sqrt{n}},$$` where `\(\bar{x}\)` is the sample mean and `\(\mu\)` the hypothetical population mean that it is tested against and `\(s\)` sample standard deviation. > Does higher value of `\(t\)` indicate higher or smaller difference? --- Let's calculate the value of test statistic. `$$t = \frac{76 - 74}{6.37 \div \sqrt{31}}$$` `$$t = 1.748$$` --- ### Test statistic `\(t\)` on t-distribution Test statistic is evaluated on t-distribution with `\(n-1\)` degrees of freedom (df). <!-- --> > Is the value of our test statistic above critical value? --- Probability of test statistic with value of 1.748 is 0.091. This 0.091 is our p-value and we chose significance level to be `\(\alpha = 0.05\)`. `$$\text{p-value} \ge 0.05 \implies H_{0}: \bar{x} = \mu$$` `$$\text{p-value} < 0.05 \implies H_{1}: \bar{x} \neq \mu$$` > So could the sample with mean tree height of 76 ft come from a population with a mean tree height of 74 ft? --- class: middle ## So... The more extreme the difference... ...the higher the value of test statistic... ...the lower the p-value... ...the lower the probability that the difference is coincidental. --- class: center middle inverse # Two samples What if we wish to compare two samples? --- ## Independent samples t-test assuming equal variances Assumptions: - normality - independence - homogeneity of variance `\(\frac{1}{2} < \frac{s_1}{s_2}<2\)` --- Example data from "Edgar Anderson's Iris Data" dataset. <!-- --> In this case `\(\frac{s_1}{s_2} =\)` 1.3793715. --- ### Hypotheses Are the mean values equal? Do these samples come from the same population? `\(H_0: \bar{x}_1 = \bar{x}_2\)` `\(H_1: \bar{x}_1 \neq \bar{x}_2\)` Let's set significance level `\(\alpha = 0.05\)`. --- ### Test statistic `\(t\)` Test statistic `\(t\)` is calculated as `$$t = \frac{\bar{x}_1 - \bar{x}_2}{se_{\bar{x}_1 - \bar{x}_2}},$$` where `\(\bar{x}_1\)` and `\(\bar{x}_2\)` are the means of samples and `\(se_{\bar{x}_1 - \bar{x}_2}\)` is the standard error of the difference of means that is calculated as follows: `$$se_{\bar{x}_1 - \bar{x}_2} = s_p \times \sqrt{\frac{1}{n_1} +{\frac{1}{n_2}}},$$` where `\(n_1\)` and `\(n_2\)` are sample sizes and `\(s_p\)` is the pooled standard deviation calculated as ... --- ### Test statistic `\(t\)` on t-distribution Value of test statistic is -12.604. Test statistic is evaluated on t-distribution with `\(n_1+n_2-2\)` df. <!-- --> --- P-value is 0 and we chose significance level to be `\(\alpha = 0.05\)`. > Do these petal samples come from the same population? ??? Different species: versicolor and virginica. --- ## Independent samples t-test not assuming equal variances Assumptions: - normality - independence Samples do not need to have homogeneous variance. The test is reliable if `\(s_1 > 2s_2\)` or `\(s_2 > 2s_1\)`. --- Example data from "Edgar Anderson's Iris Data" dataset. <!-- --> In this case `\(\frac{s_1}{s_2} =\)` 7.3216944. --- ### Hypotheses Are the mean values equal? Do these samples come from the same population? `\(H_0: \bar{x}_1 = \bar{x}_2\)` `\(H_1: \bar{x}_1 \neq \bar{x}_2\)` Let's set significance level `\(\alpha = 0.05\)`. --- ### Test statistic `\(t\)` Test statistic is the same as for Student test: `$$t = \frac{\bar{x}_1 - \bar{x}_2}{se_{\bar{x}_1 - \bar{x}_2}},$$` where `\(\bar{x}_1\)` and `\(\bar{x}_2\)` are the means of samples and `\(se_{\bar{x}_1 - \bar{x}_2}\)` is the standard error of the difference of means that is calculated as follows: `$$se_{\bar{x}_1 - \bar{x}_2} = \sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}},$$` where `\(s_1\)` and `\(s_2\)` are unbiased standard deviations of the samples. --- ### Test statistic `\(t\)` on t-distribution Value of test statistic is 39.493. Test statistic is evaluated on t-distribution where df is calculated using a complicated formula. <!-- --> --- P-value is 0 and we chose significance level to be `\(\alpha = 0.05\)`. > Do these petal samples come from the same population? ??? Different species: versicolor and setosa. --- class: middle center inverse # Paired samples What if our samples are not independent? --- ## Paired-samples t-test Assumptions: - normality Let's set significance level `\(\alpha = 0.05\)`. --- What is paired data? | extra|group |ID | extra|group |ID | |-----:|:-----|:--|-----:|:-----|:--| | 0.7|1 |1 | 1.9|2 |1 | | -1.6|1 |2 | 0.8|2 |2 | | -0.2|1 |3 | 1.1|2 |3 | | -1.2|1 |4 | 0.1|2 |4 | | -0.1|1 |5 | -0.1|2 |5 | | 3.4|1 |6 | 4.4|2 |6 | | 3.7|1 |7 | 5.5|2 |7 | | 0.8|1 |8 | 1.6|2 |8 | | 0.0|1 |9 | 4.6|2 |9 | | 2.0|1 |10 | 3.4|2 |10 | --- Let's see the effect of different drugs on increase in hours of sleep. Data is from dataset "Student's Sleep Data". <!-- --> ??? Effect of different drugs --- ### Hypotheses Are the mean values equal? Do these samples come from the same population? Would we also observe the increase in hours of sleep in population? `\(H_0: \bar{x}_1 = \bar{x}_2\)` `\(H_1: \bar{x}_1 \neq \bar{x}_2\)` Let's set significance level `\(\alpha = 0.05\)`. ??? If different populations, then increase also occurs in population. Draw! --- ### Test statistic `\(t\)` Test statistic `\(t\)` is calculated as `$$t = \frac{\hat{D}}{s_\Delta\div \sqrt{n_1 + n_2}},$$` where `\(s_\Delta\)` is difference in standard deviation expressed as `\(s_\Delta = s_1 - s_2\)` and `\(\hat{D}\)` is the mean of differences between paired values calculated as `$$\hat{D} = \frac{1}{n} \sum_{i=1}^i{(X_{i1} - X_{i2})}.$$` ??? We're essentially testing if the difference or change is extreme enough. --- ### Test statistic `\(t\)` on t-distribution Value of test statistic is -4.062. Test statistic is evaluated on t-distribution with `\(n-1\)` df where `\(n\)` is the number of pairs. <!-- --> --- P-value is 0.003 and we chose significance level to be `\(\alpha = 0.05\)`. > Did the hours of sleep increase only in our sample or also in population? --- class: middle center inverse # One-tailed tests What if we are not interested in difference but wish to know if one parameter is larger or smaller than another? --- ### Hypotheses If we wish to test if mean of sample ( `\(\bar{x}\)` ) is greater than hypothetical population mean ( `\(\mu\)` ), then our hypotheses are the following: `\(H_0: \bar{x} \le \mu\)` `\(H_1: \bar{x} \gt \mu\)` If we wish to test if mean of one sample ( `\(\bar{x}_1\)` ) is greater than mean of another sample ( `\(\bar{x}_2\)` ) , then our hypotheses are the following: `\(H_0: \bar{x}_1 \le \bar{x}_2\)` `\(H_1: \bar{x}_1 \gt \bar{x}_2\)` --- ### Test statistic `\(t\)` on t-distribution (one-tailed) Value of test statistic is -4.062. <!-- --> Now we observe only one side of the distribution. Is t-statistic above the critical value? ??? For \alpha = 0.05 we need to use critical value of -1.645 for lower-tailed test. --- P-value is 0.001 and we chose significance level to be `\(\alpha = 0.05\)`. `\(H_0: \bar{x} \le \mu\)` `\(H_1: \bar{x} \gt \mu\)` > Hours of sleep increased in our sample. Did the hours of sleep in population actually decrease? ??? P-value is high. So the probability that the difference is random is high. --- class: center middle inverse # Nonparametric tests What if our data is not normally distributed? --- ## Normal distribution Commonly used continuous probability distribution due to *central limit theorem*. Many methods assume random variables to be normally distributed. Symmetric and bell-shaped. Characterized by parameters mean ( `\(\mu\)` ) and variance ( `\(\sigma^2\)` ). ( `\({\mathcal{N}}(\mu,\sigma^{2})\)` ). For standard normal distribution mean is 0 and variance 1 ( `\({\mathcal{N}}(0,1)\)`. --- 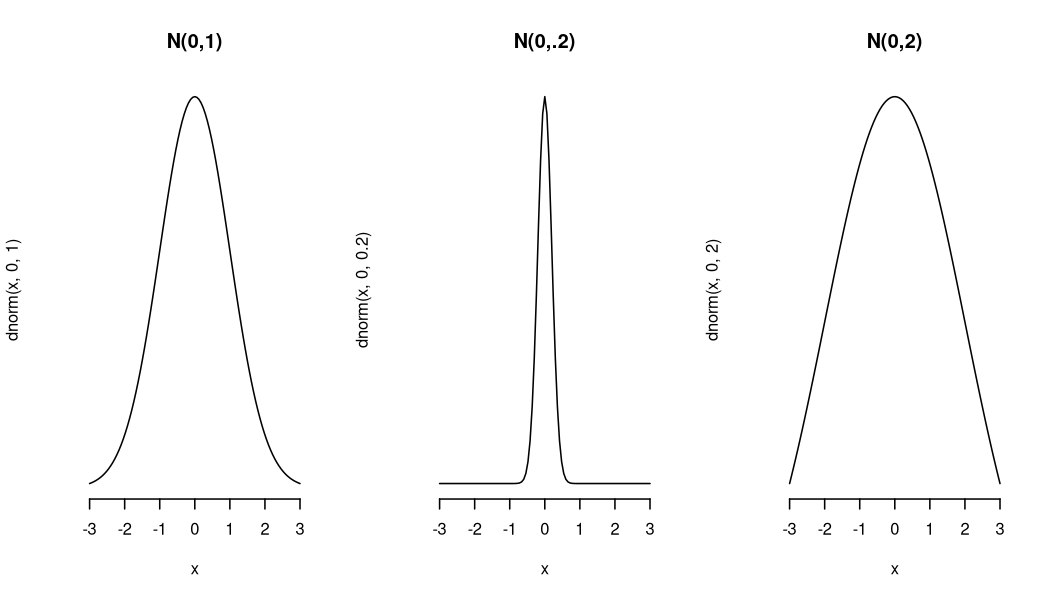<!-- --> --- ### How to test normality? #### QQ plot On these scatterplots empirical quantiles of data are plotted against theoretical quantiles that represent normal distribution. Let's use some data on rocks from "Measurements on Petroleum Rock Samples" to test normality. --- <!-- --> -- > Your conclusion? --- <!-- --> -- > Conclusion? --- #### Shapiro-Wilk test Let's set significance level `\(\alpha = 0.05\)`. We test if the distribution of values is different from normal distribution. So the hypotheses are the following: `\(H_0\)`: Data is normally distributed `\(H_1\)`: Data is not normally distributed --- For test statistic `\(W\)` higher value and thus p-value below `\(\alpha\)` indicates non-normality. -- ```r shapiro.test(rock$area) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: rock$area ## W = 0.97944, p-value = 0.5555 ``` > Conclusion? -- ```r shapiro.test(rock$shape) ``` ``` ## ## Shapiro-Wilk normality test ## ## data: rock$shape ## W = 0.90407, p-value = 0.0008531 ``` > Conclusion? --- ## Mann-Whitney U test Compare two independent samples that are not necessarily normally distributed. Test assumes independence of samples. It also means that observations need to be **unpaired**. --- Data on number of breaks and type of wool from "The Number of Breaks in Yarn during Weaving". The median number of breaks for wool A is 26 and for wool B 24. -- .pull-left[ <!-- --> ] -- .pull-right[ ``` ## ## Shapiro-Wilk normality test ## ## data: warpbreaks$breaks[warpbreaks$wool == "A"] ## W = 0.89698, p-value = 0.01141 ``` ``` ## ## Shapiro-Wilk normality test ## ## data: warpbreaks$breaks[warpbreaks$wool == "B"] ## W = 0.91554, p-value = 0.03087 ``` ] -- > Are these distributions different? ??? Different tests --- ### Hypotheses Are the mean values equal? Do these samples come from the same population? Does the number of breaks in yarn depend on the type of wool? `\(H_{0}\)`: Distributions (medians) of both samples are the same. `\(H_{1}\)`: Distributions (medians) of samples are different. Formal definition of `\(H_{0}\)`: A randomly selected value from one sample is equally likely to be less than or greater than a randomly selected value from a second sample. Let's set significance level `\(\alpha = 0.05\)`. ??? Draw popluation A and population B. --- ### Test statistic `\(U\)` Test statistic `\(U\)` is calculated as `$$U = \sum^n_{i=1} \sum^m_{j=1} S(X_1, X_2),$$` where `\(n\)` are rows and `\(m\)` columns of a matrix `\(S(X_1, X_2)\)` described as below. `$$S(X_1, X_2) = \begin{cases} 1 & \text{if } Y < X\\ \frac12 & \text{if } Y = X\\\ 1 & \text{if } Y > X\ \end{cases}$$` ??? Basically, we compare all values and count the times when values from one sample are higher than values from another sample. The `\(U\)` is just the count of these differences. --- ### Test statistic `\(U\)` on normal distribution Value of test statistic is 431. Test statistic is evaluated on Wilcoxon distribution that approaches normal distribution if `\(n>20\)`. -- P-value is 0.253 and we chose significance level to be `\(\alpha = 0.05\)`. > Does the number of breaks in yarn depend on the type of wool? --- ## Wilcoxon signed-rank test This is similar to Mann-Whitney U test but used for **paired** samples. Test assumes that observations are **paired**, but pairs are independent. --- Let's explore "Weight versus age of chicks on different diets" and compare weights on day 2 and 4. <!-- --> ??? Two different time periods but same chicken. --- ### Hypotheses Did the weight increase only in our sample or also in a population? Is the increase in weight significant? `\(H_{0}\)`: Distributions (medians) of both samples are the same. `\(H_{1}\)`: Distributions (medians) of samples are different. Let's set significance level `\(\alpha = 0.05\)`. --- ### Test statistic `\(W\)` The W statistic is calculated as: `$$W = \sum^n_{i = 1}(sgn(x_{1i}x_{2i}) \times R_i),$$` where `\(sgn(x_{1i}x_{2i})\)` is sign function (1 for positive difference, -1 for negative) and `\(R_i\)` is the rank of absolute difference. ??? Basically, we are comparing how different is the ranking of values between two samples. The `\(W\)` is just the sum of ranked differences. --- ### Test statistic `\(U\)` on normal distribution Value of test statistic is 0. Test statistic is evaluated on Wilcoxon distribution that approaches normal distribution if `\(n > 20\)`. -- P-value is 0 and we chose significance level to be `\(\alpha = 0.05\)`. > Did the weight increase only in our sample or also in a population? --- ## Kolmogorov-Smirnov test This test is equivalent to Mann-Whitney U test, although the calculation is very different. --- Example data on "The Effect of Vitamin C on Tooth Growth in Guinea Pigs". Let's compare two supplement types. <!-- --> --- ### Hypotheses Is the tooth length different for different types of supplements? Do the supplements have a different effect? `\(H_{0}\)`: Distributions of both samples are the same. `\(H_{1}\)`: Distributions of samples are different. Let's set significance level `\(\alpha = 0.05\)`. --- ## Cumulative distribution function (CDF) <!-- --> --- ### Test statistic `\(D\)` This is simply the maximum absolute difference between two cumulative distribution functions. Value of test statistic is 0.333. <!-- --> --- P-value is determined by the extremity of the D-statistic on Kolmogorov distribution. P-value is 0.071 and we chose significance level to be `\(\alpha = 0.05\)`. > Do the supplements have a different effect? --- class: center middle inverse # Practical application --- Load data as follows: 1. Download the data set "barley" from the course notes. 2. Go to cloud.jamovi.org. 3. Open the data set in Jamovi. 4. Use only rows for year 1932 (filter `year == 1932`). Conduct tests about the yield in population. 1. Are the weights normally distributed? 2. Are the measurements of weights independent? 3. Which test should we use? > Could the yield in population be greater than 30? ??? If we had kept both years, then the data would not be independent. --- Use data set "Griliches" from the course notes. Conduct tests to see if wages for individuals changed. 1. Are wages normally distributed? 2. Are the measurements of wages independent? 3. Which test should we use? > Is the mean of wage during first observation different from wage in 1980? > > Could wages actually have decreased? ??? Paired samples test --- Use data set "computers" from the course notes. Conduct tests to see what determines the price of computers. 1. Are the prices normally distributed? 2. Are the prices independent? 3. Which test should we use? > Does the price depend on the presence of CD-ROM? > > Does the incusion multimedia kit influence the price? > > Are computers manufactured by premium firms more expensive? ??? Non-parametric test --- class: inverse